This article was first published in the June 2019 edition of M500,
the mathematics magazine of The Open University

Flippin' Functions
Title for Flippin' Functions

Function Flow Diagrams Taken To The Max

Martin Hansen

 3rd July 2019 

When I first became a secondary school teacher of mathematics I rather liked the visual approach to writing down the inverse of a function. A typical GCSE examination question would begin by presenting a flow chart and ask what function it described. For example:

Figure 01

Readers of M500 will have no difficulty in realising that the function described by the diagram by flowing left to right as indicated by the arrows is:

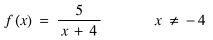
Figure 02

Rather attractively, clever pupils were able to write down the inverse function by simply moving against the flow, remembering that the inverse of multiplication is division, and of addition is subtraction. Taking a reciprocal is self inverse.
Thus:

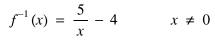
Figure 03

For some pupils it proved helpful to make them draw the reversed flowchart first:

Figure 04

My enthusiasm for this visual approach of obtaining the inverse of a function lessened when a colleague told me it failed as the functions became more complicated, and gave me, as an example:

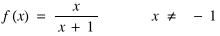
Figure 05

The problem is having an x in more than one place. The mainstream algebraic approach of, effectively, making x the subject of the formula seemed the only way to cope with such questions. Recently, however, when looking at this function with an A-Level class I began to wonder if I could, after all, get the flow charting method to work. Some simple, if mildly sneaky, algebra was employed to get the x into just one place:

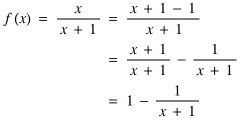
Figure 06

A flowchart followed:

Figure 07

which, step by step, I can demonstrate is doing what it should:

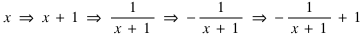
Figure 08

This can be reversed:

Figure 09

which, step by step, is doing this:

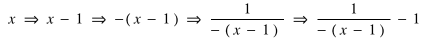
Figure 10

and finally some algebraic manipulation;

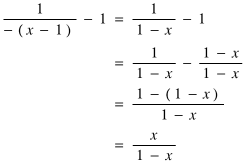
Figure 11

got to the answer that I knew, from the algebraic approach, was correct:

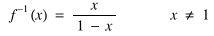
Figure 12

I'm going to conclude with a challenge.
•  Can this 'foot in the door' be developed to tackle the 'worst case' GCSE inverse function questions which are of the form of a Möbius transformation:

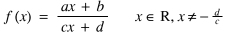
Figure 13

but with a, b, c and d restricted to being integers.

•   What other awkward functions can be handled, keeping in mind that to have an inverse, a function must be one-to-one ?

•   For example, what about:

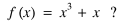
Figure 14 

© June 2019, M500, the mathematics magazine of The Open University
Licensed to Number Wonder, July 2019